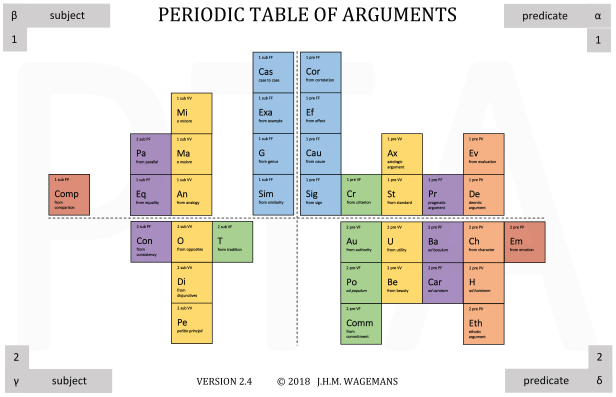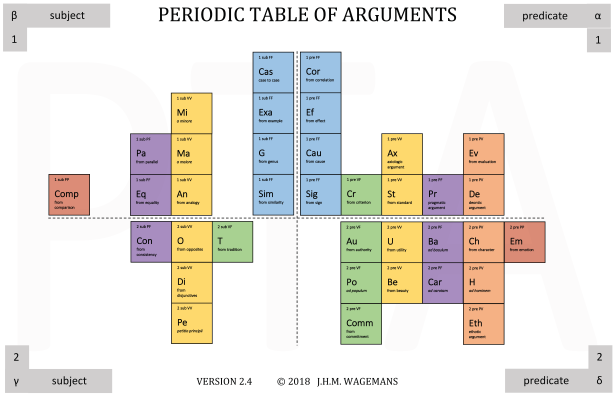
The Periodic Table of Arguments (PTA).
The Periodic Table of Arguments (PTA) is a comprehensive overview of the techniques people use to persuade others of their point of view (Wagemans 2016, 2017, 2019b). The table is inspired by the classical disciplines dialectic (the art of philosophical debate) and rhetoric (the art of public speaking). It modernizes their traditional descriptions of argument schemes, fallacies, and other means of persuasion by unifying them in an overarching argument classification framework.
Compared to traditional classifications of argument, the PTA has a fully explicit theoretical rationale and can be characterized as a factorial typology of argument. This means that each basic type of argument is described as a unique combination of independent features. In the present version of the PTA, an argument type is described as (1) a first-order or a second-order argument; (2) a predicate argument or a subject argument; and (3) an instantiation of one out of nine possible combinations of types of statement. The theoretical framework thus allows for 2 x 2 x 9 = 36 basic types of argument.
Another difference with traditional classifications is that the PTA is specifically designed to enable a formalization of the characteristics of the various types of argument. The PTA takes an argument to consist of exactly one premise and one conclusion, both of which are expressed by means of a statement containing a subject and a predicate. Closely following logical conventions, subjects are indicated with letters a, b, etc., predicates with letters X, Y, etc., and complete propositions with letters p, q, etc.
Based on these distinctions, it is possible to determine the type of any argument expressed in natural language (Wagemans, 2019a). The analyst first determines the ‘argument form’, which notion comprises the first two features mentioned above. The argument The suspect was driving fast, because he left a long trace of rubber on the road, for instance, has the form ‘a is X, because a is Y’ and can therefore be characterized as a first-order predicate argument. The third feature mentioned above, the specific combination of types of statements, is covered by the notion of ‘argument substance’. Its determination takes place in terms of a tripartite typology consisting of statements of fact (F), statements of value (V), and statements of policy (P). Given these possibilities, the conclusion and premise of the argument substantiate one of the following nine combinations of types of statements: PP, PV, PF, VP, VV, VF, FP, FV, FF. The example just mentioned can be characterized as an FF argument, since driving fast and leaving a long trace of rubber on the road can both be labelled as statements of fact.
The identification of the argument type instantiated by any argument expressed in natural language makes it possible to derive the underlying mechanism of the argument, which is crucial for the subsequent evaluation of its quality. Since The suspect was driving fast, because he left a long trace of rubber on the road can be identified as a first-order predicate argument combining a statement of fact with another statement of fact (1 pre FF), it is clear that this argument is based on a relation between two facts, i.c., the relation of cause and effect between driving fast and leaving a long trace of rubber on the road.
Apart from being an appropriate means for the analysis and evaluation of persuasive discourse, the table can also be used as a heuristic device for generating premises in support of any given conclusion.
The argument classification framework of the PTA is based on clear standards for distinguishing between the types of argument and provides formal(izable) descriptions of their properties. For these reasons, the PTA is especially suitable as a point of departure for formal linguistic and computational research into the various ways in which people try to convince others of their point of view. So far, it has been used in various research projects, among which the first and largest annotation of argument schemes in a dialogical corpus (Visser et al., 2018) and the Adpositional Argumentation project (Gobbo & Wagemans 2019a, 2019b, to appear), which is aimed at developing a high precision tool for representing the linguistic and pragmatic features of argumentation.
References
Gobbo, F., & Wagemans, J.H.M. (to appear). Adpositional Argumentation (AdARg): A new method for representing linguistic and pragmatic information about argumentative discourse. Proceedings 13e Journées de l’Intelligence Artificielle Fondamentale (JIAF 2019).
Gobbo, F., & Wagemans, J.H.M. (2019). A method for reconstructing first-order arguments in natural language. In P. Dondio & L. Longo (Eds.), Proceedings of the 2nd Workshop on Advances in Argumentation in Artificial Intelligence (AI^3 2018), co-located with the 17th International Conference of the Italian Association for Artificial Intelligence (AI*IA 2018), Trento, Italy, November 20-23, 2018 (pp. 27-41). Aachen: Sun SITE Central Europe. A method for reconstructing first-order arguments in natural language.
Gobbo, F., & Wagemans, J.H.M. (2019). Building argumentative adpositional trees: Towards a high precision method for reconstructing arguments in natural language. In B.J. Garssen, D. Godden, G.R. Mitchell & J.H.M. Wagemans (Eds.), Proceedings of the Ninth Conference of the International Society for the Study of Argumentation (pp. 408-420). Amsterdam: SIC SAT.
Visser, J., Lawrence, J., Wagemans, J.H.M., & Reed, C.A. (2018). Revisiting computational models of argument schemes: Classification, annotation, comparison. In S. Modgil, K. Budzynska & J. Lawrence (Eds.), Computational Models of Argument: Proceedings of COMMA 2018 (pp. 313-324). (Frontiers in Artificial Intelligence and Applications; Vol. 305). Amsterdam: IOS Press. DOI: Revisiting Computational Models of Argument Schemes: Classification, Annotation, Comparison.
Wagemans, J.H.M. (2016). Constructing a Periodic Table of Arguments. In P. Bondy & L. Benacquista (Eds.), Argumentation, Objectivity, and Bias: Proceedings of the 11th International Conference of the Ontario Society for the Study of Argumentation (OSSA), 18-21 May 2016 (pp. 1-12). Windsor, ON: OSSA.
Wagemans, J.H.M. (2017). Periodic Table of Arguments: The building blocks of persuasive discourse. 47 pages. Published online December 9, 2017. Periodic Table of Arguments (PTA).
Wagemans, J.H.M. (2019a). Argument Type Identification Procedure (ATIP). 4 pages. Published online January 28, 2019.
Wagemans, J.H.M. (2019b). Four basic argument forms.